МЕТОДЫ ВЫДЕЛЕНИЯ НЕОДНОРОДНОСТЕЙ ВРЕМЕННЫХ РЯДОВ

Рассматривается задача выделения неоднородностей стохастических временных рядов, т.е. задача фиксации изменений тех или иных вероятностных характеристик этого дискретного процесса, либо обнаружение такого изменения. В принципе для решения такого рода задач обычно используются классические методы проверки статистических гипотез, методы дисперсионного анализа и т.п. Однако их применение требует большого объема априорной информации, поскольку в основе их лежат, как правило, предпосылки о статистической независимости наблюдений и определенном виде функции распределения вероятностей. На практике зачастую такая информация отсутствует, а для ее получения требуется проведение весьма громоздких предварительных исследований. В такой ситуации представляется предпочтительным иной подход, основанный на использовании процедур линейной фильтрации.

Далее данная задача рассматривается в условиях следующих предпосылок:

Предлагается использовать различные процедуры выделения для разных направлений изменения дисперсии.

При ее увеличении эффективным оказывается следующий порядок действий:

Эффективность предложенной процедуры обусловлена тем, что математическое ожидание , и различие между и будет увеличиваться при любом изменении математического ожидания на интервале L.

Возможен и другой альтернативный вариант обработки временного ряда. Он основан на предложенном в [1] скользящем вычислении среднеквадратических отклонений трех - пяти соседних наблюдений. Такая обработка позволяет подчеркнуть наличие кратковременных изменений дисперсии процесса. Предлагается дополнить эту обработку фильтрацией с помощью упоминавшегося ранее фильтра скользящего среднего шириной .

Проиллюстрируем сказанное примером. В качестве анализируемого процесса используется временной ряд, наблюдаемый при регистрации процесса радиоактивного распада, подвергнутого внешнему воздействию [1]. На рис. 1а) представлен фрагмент этого ряда; там же условно отмечен временной интервал, в течение которого осуществлялось внешнее воздействие, имеющее в данном случае двухступенчатый характер. На рис. 1б) изображена кривая, полученная в результате скользящего сглаживания среднеквадратических отклонений трех соседних наблюдений.

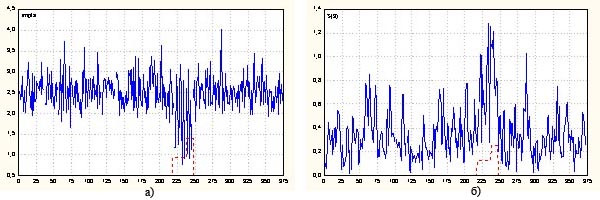
Рис. 1.

Очевидно, что, хотя можно отметить факт увеличения дисперсии процесса во время воздействия; однако характерные особенности такого изменения выражены не очень отчетливо. Кроме того, имеются и ложные всплески, которые можно интерпретировать как увеличение дисперсии, когда воздействие отсутствует.

На рис. 2а) представлен результат обработки временного ряда с помощью описанного выше алгоритма. Ширина фильтра скользящего среднего L = 11 выбрана примерно равной длительности второй, более короткой ступени воздействия. В данном случае влияние воздействия прослеживается уже абсолютно четко, включая особенности, обусловленные двухступенчатостью воздействия.

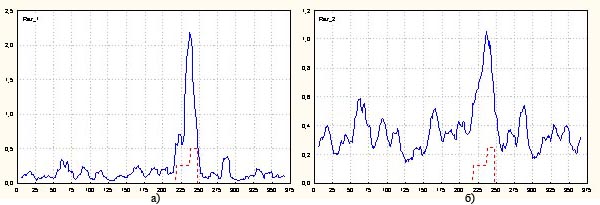
Рис. 2.

На рис. 2б) представлены результаты альтернативного способа обработка, когда кривая рис. 1б) дополнительно сглаживалась фильтром скользящего среднего с L = 11. Результат здесь также получается вполне приемлемым, хотя и несколько уступающим предыдущему.

Для случая уменьшения дисперсии предлагается видоизмененный алгоритм обработки, поскольку здесь изменение дисперсии может компенсироваться слагаемым . Для этого случая целесообразно получать раздельные оценки математических ожиданий, т.е. получение наряду с и оценки . Тогда и операция центрирования также должна производиться раздельно по участкам без воздействия (фон) и при наличии воздействия: , если , и , если . После этого реализуется п. 3 предыдущей процедуры. Очевидно, что в общем случае выделение неоднородности процесса, когда его дисперсия уменьшается, является более трудной задачей по сравнению со случаем увеличения дисперсии. Для случая уменьшения дисперсии без каких либо изменений применим и альтернативный алгоритм обработки.

Приведем характерный пример, также заимствованный из [1]. В данном случае воздействие, приводящее к предполагаемому уменьшению дисперсии, имеет длительность, равную 7 единицам, и носит одноступенчатый характер. На рис. 3а) и 3б) приведены исходная реализация и результаты обработки скользящим усреднением среднеквадратических отклонений трех соседних наблюдений. На рис. 4а) и 4б) изображены кривые, полученные с помощью предложенного и альтернативного алгоритмов при L = 5. В данном случае альтернативный алгоритм дает даже несколько лучший результат.

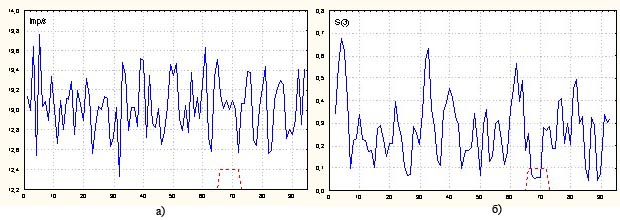
Рис. 3.

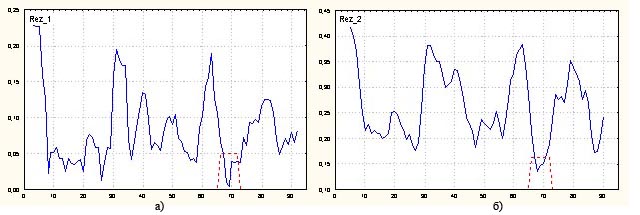
Рис. 4.

Очевидно, что применение рассмотренных алгоритмов обработки неоднородных данных позволяет более точно и наглядно подтвердить факт значимого влияния внешнего воздействия на наблюдаемый процесс (в примерах - это влияние на процесс радиоактивного распада или на средства его регистрации).

Возможен другой вариант исходной постановки задачи, более сложный с точки зрения ее решения, а именно, когда временной интервал появления неоднородностей неизвестен и необходимо обнаружить появление изменения свойств наблюдаемого процесса.

Для решения данной задачи в режиме реального времени могут быть использованы оптимальные алгоритмы обнаружения "разладки" процесса, обладающие наилучшими свойствами с точки зрения быстродействия при фиксированном интервале между ложными тревогами.

ЛИТЕРАТУРА:

1. Каравайкин А.В. Управление процессом радиоактивного распада неэлектромагнитным информационным воздействием. - ИНФОРМАТИКА, СОЦИОЛОГИЯ, ЭКОНОМИКА, МЕНЕДЖМЕНТ, Сб. научных трудов, часть 1, НОУ "Академия менеджмента инноваций", Москва, 2005, с. 85-92.